COMP3014 Network Simulation Project
Problem Statement
PDF Version of this Solution
COMP3014_Network_Simulation_Project.pdf
Abstract
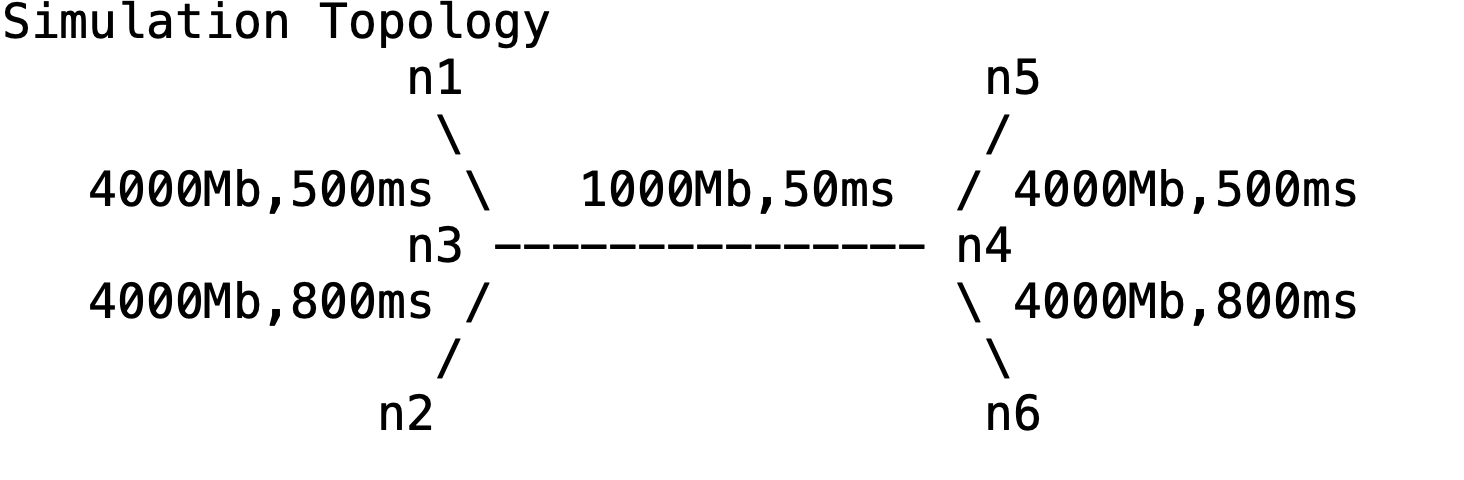
This experiment uses ns2 to construct a simulation scenario comprising one node and five different line bandwidths and latency. Specifically, N3 and N4 nodes serve as a router to connect the networks. The queue size from N3 to N4 is $10$. From the network topology, the bandwidth of link $N3 \sim N4$ is the network’s bottleneck. In fact, the main factors that influence the performance the queue size and network latency. In our experiments, we analyze the factors of 4 TCP congestion control algorithms that could impact the packet loss, Goodput rate and end-to-end delay. Moreover, we adjust the parameters of the experiments to demonstrate the reasonability of our proposed assumptions. Meanwhile, we compared the performance of RED and DropTail. Then we further analyze the reasons for such different performances of RED and DropTail. Furthermore, we conduct experiments to determine the best fit scenario of RED and DropTail.
Project Introduction
Part A: Experimental Environment Setup
Preparing the Ubuntu OS as a virtual machine
-
Download and install VMWare workstation
-
Download the Ubuntu ISO image.
-
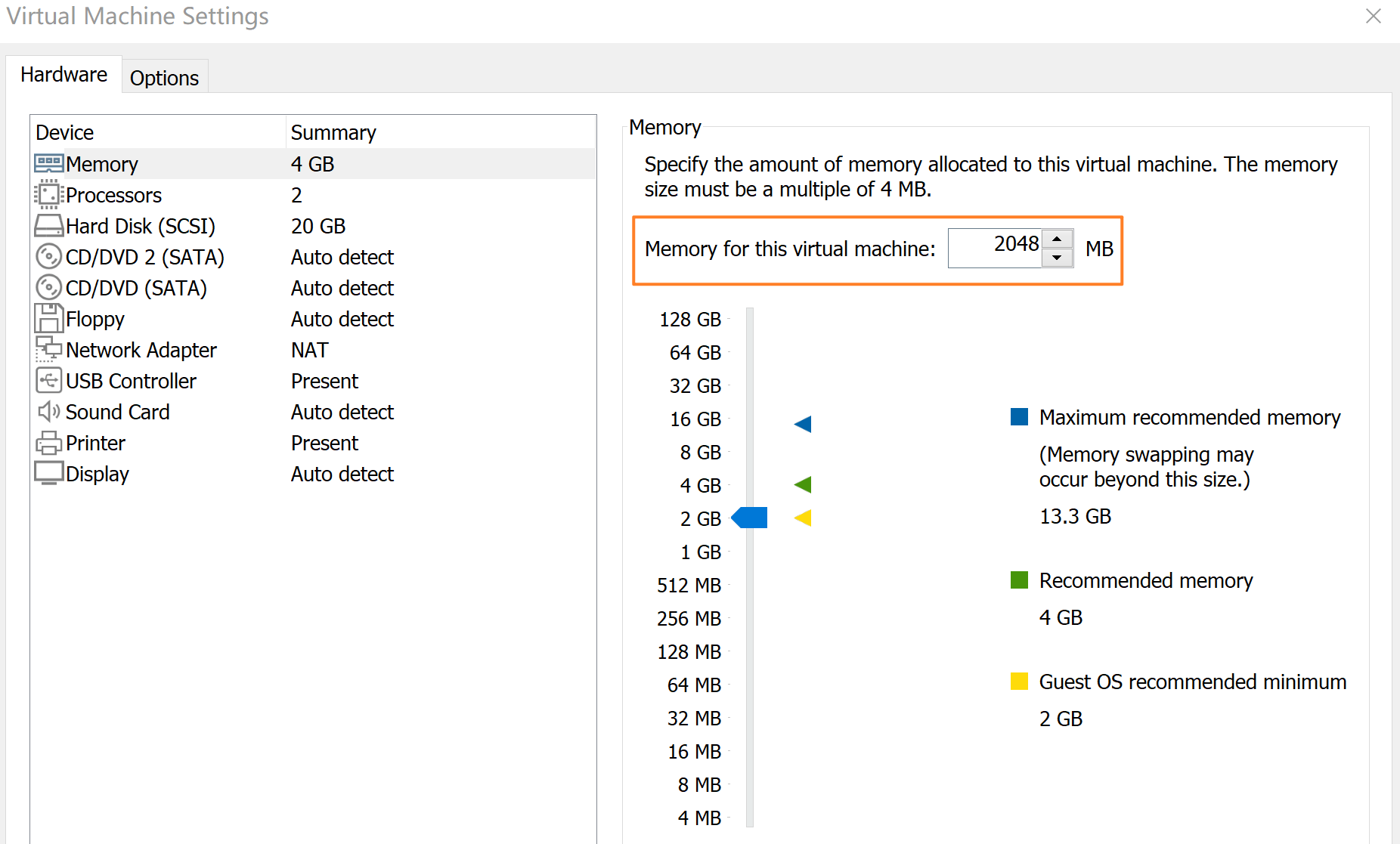
Create a new virtual machine in VMWare and set memory size (RAM) to 2048 MB.
-
Create virtual hard disk and select VDI type of hard disk file and dynamically allocated hard disk file size.
-
Set 20 GB of file size. When the virtual machine is ready - set 2 CPUs, and the video memory to 128MB in the Display tab.
-
Install Ubuntu system
NS2 Installation
-
Install ns2, NAM (Network Animator), and Tcl (Tool Command Language) and verify the installation of ns2
-
Clone the project Git repository and Run the test file
Part B: Network Simulator Setup
Trace File, Trace Data Analyzer Script and Plotting
The trace file, which may contain hundreds of lines, records the simulation’s outcome in the event’s format. Consequently, we use scripting languages such as awk or Python to extract meaning (analyze) from the trace file.
cat out.tr | // Read out.tr file and pipe the output to the next command
grep " 2 3 cbr " | // Look for 2 (from) 3 (to) cbr (type) line
grep ^r | // Select lines start with letter 'r' (receive)
column 1 10 | // Select column 1 - 10
awk '{dif = $2 - old2; // check whether there is a different in time
if(dif==0) dif = 1;
if(dif > 0) { // calculate jitters
printf("%d\t%f\n", $2, ($1 - old1) / dif); old1 = $1; old2 = $2}
}'
> jitter.txt // REDirect output to 'jitter.txt'
Python library to Analyze .tr files
TCP Congestion Control Algorithm Simulation
Why does the plot look very unstable at the beginning of the simulation?
End-to-End Delay
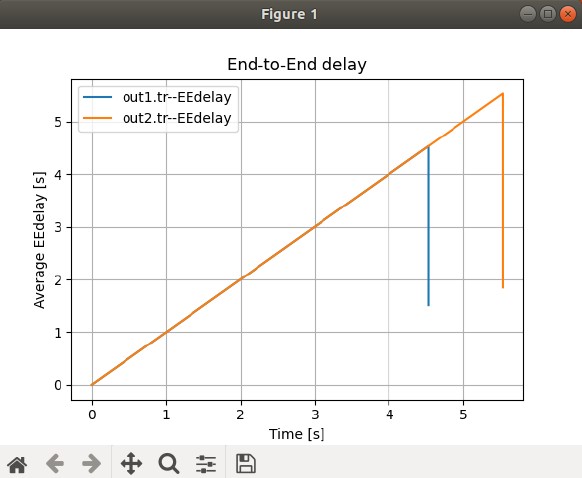
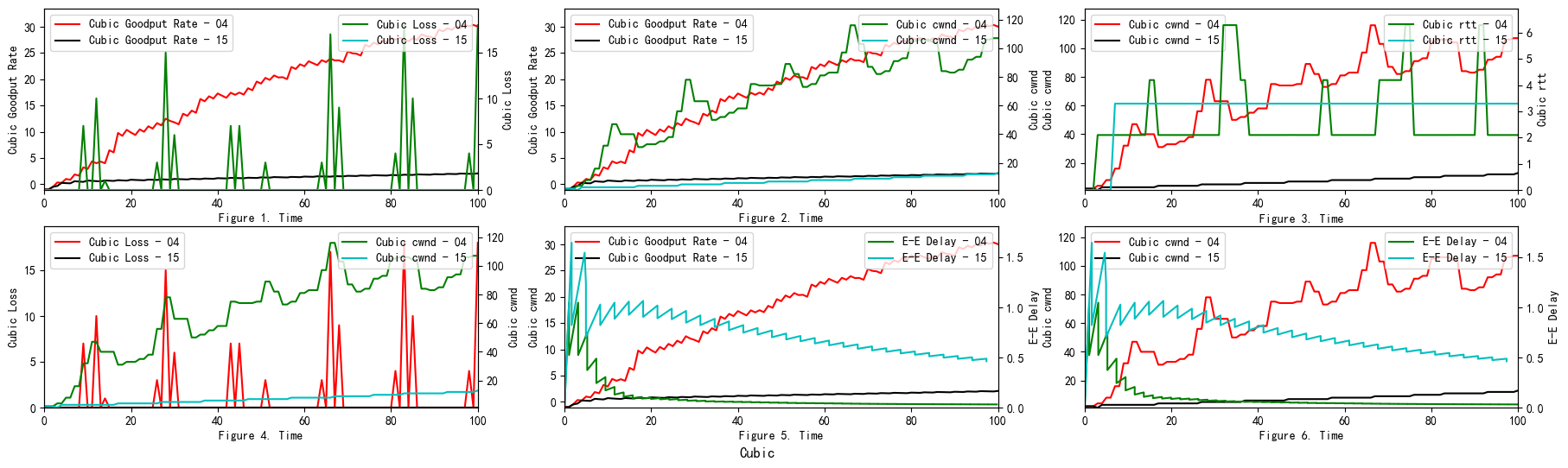
It is important to note that the End-to-End Delay measured at the N4 node changes steeply with time (see Figure 1 and Figure 2). We propose two reasons for that steep change. Firstly, there is some time difference between each send due to delayed ACK response. Secondly, two sources may affect the end-to-end delay. One source is packets from N1 with a delay of $500ms + 50ms$. Another source is packets from N2 with a delay of $800ms + 50ms$. To demonstrate our supposition’s validity, we conducted the following comparison experiments.
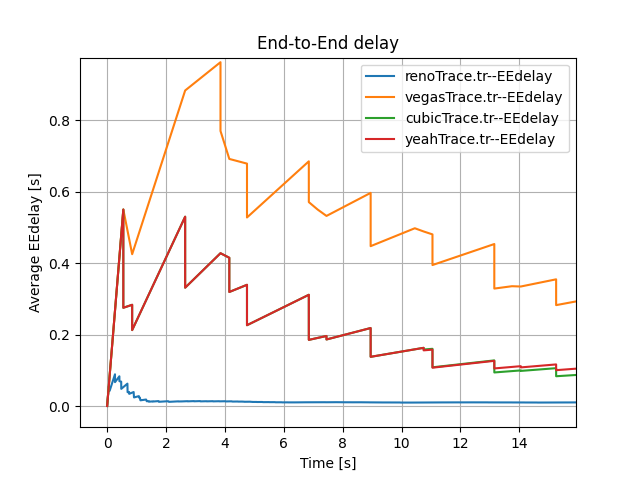
For one thing, there is some time difference between each send. This is because senders should wait until ACK is received or timeout and then send a new packet. This includes an extra waiting time. All of these reasons may affect the end-to-end delay.
For flow 1 (from $N_1$ to $N_5$),
$$ T_{odd} =\underbrace{T(N_1 \sim N_3) + T(N_3 \sim N_4)}_{Sending} $$
For flow 2 (from $N_2$ to $N_6$),
$$ T_{odd} = \underbrace{T(N_2 \sim N_3) + T(N_3 \sim N_4)}_{Sending} $$
Thus, the difference for these two measured time is
$$ T(N_4 \sim N_5) + \underbrace{T(N_5 \sim N_4) + T(N_4 \sim N_3) + T(N_3 \sim N_1)}_{Waiting ACK \downarrow} $$
for flow 1 and
$$ T(N_4 \sim N_6) + \underbrace{T(N_6 \sim N_4) + T(N_4 \sim N_3) + T(N_3 \sim N_2)}_{Waiting ACK \downarrow} $$
for flow 2.
For another, we use the following codes to show how the E-E delay changes with time if we include only one source. The first below block closes the N2 source, and the second below block closes the N1 source.
//$ns at 0.0 "$myftp2 start"
$ns at 0.0 "$myftp1 start
$ns at 0.0 "$myftp2 start"
//$ns at 0.0 "$myftp1 start
When we only include a single source, the trends change regularly, which is different to our previous random and steep changes (see Figure 4).
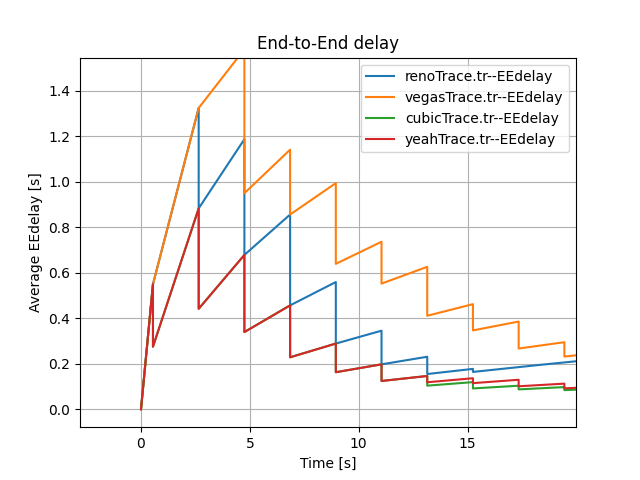
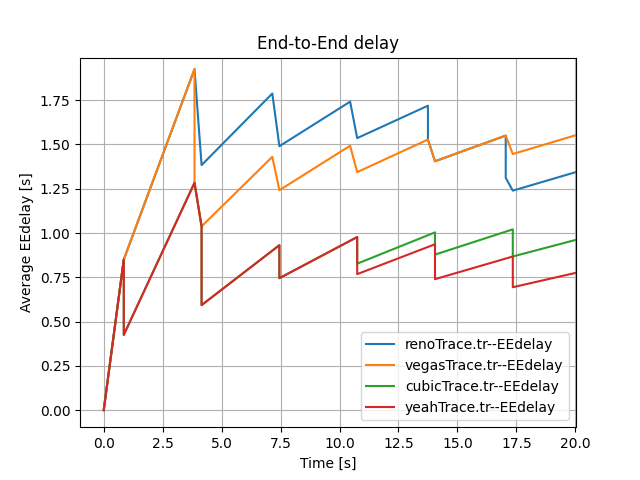
Now we take the Reon TCP congestion control algorithms as an example, which also applies to other congestion control algorithms.
Overall, the above experiments demonstrate our assumption that both two sources and waiting time leads to the steep trends of Figure 1 and Figure 2.
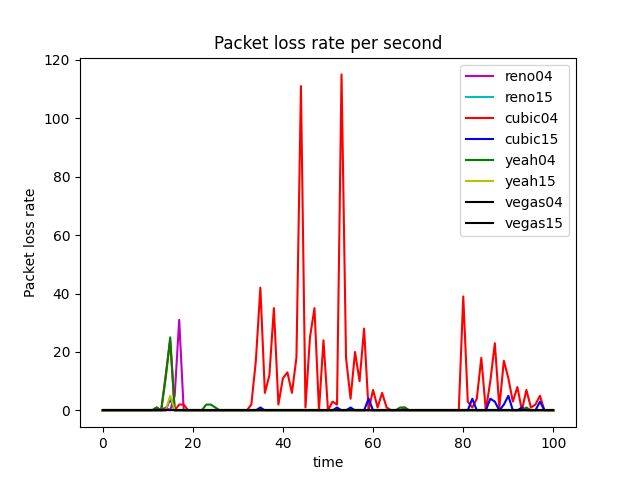
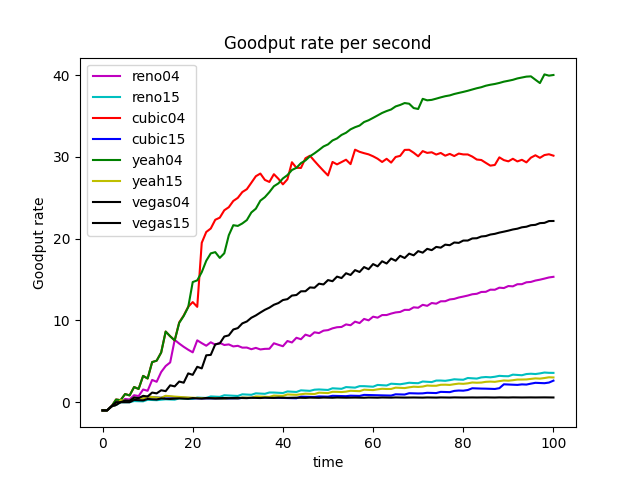
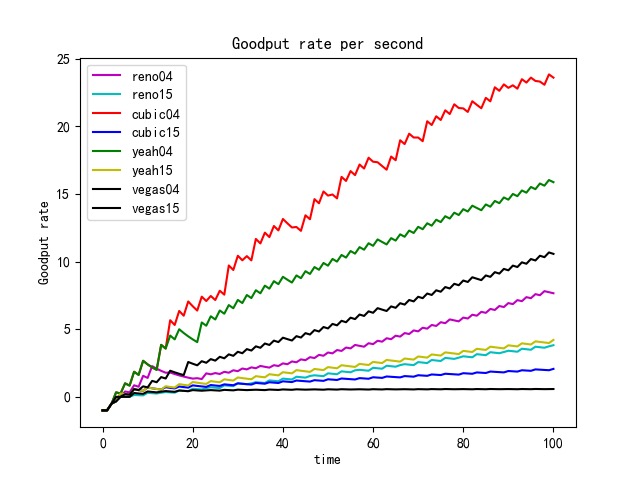
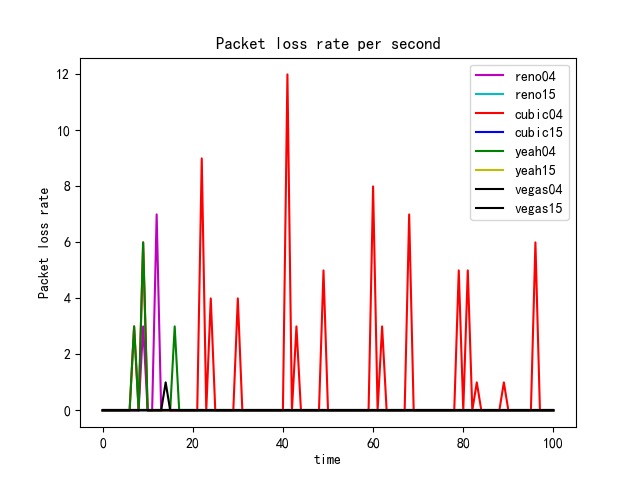
GoodPut Rate and Packet Loss Rate
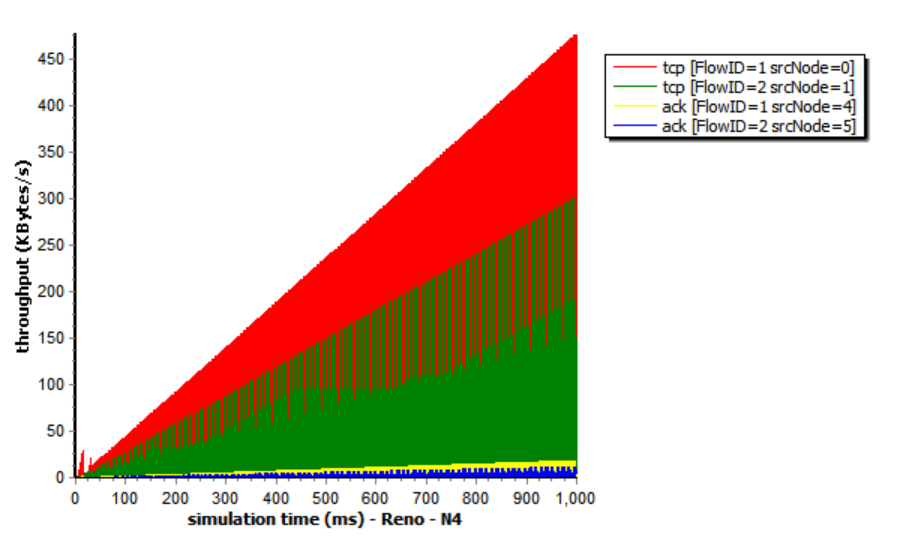
Take TCP Reno Congestion Control Algorithm as an Example
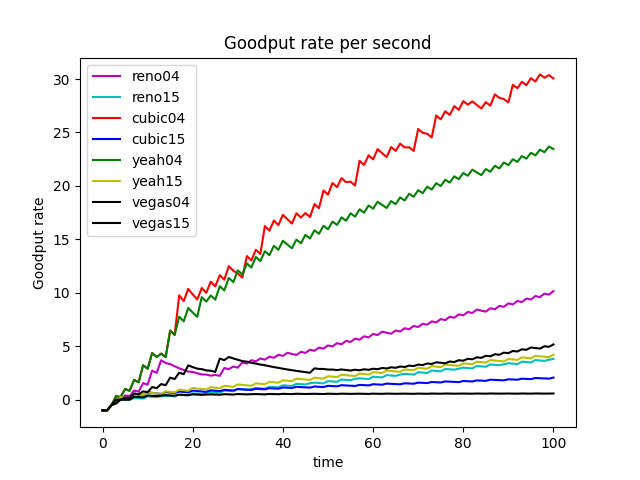
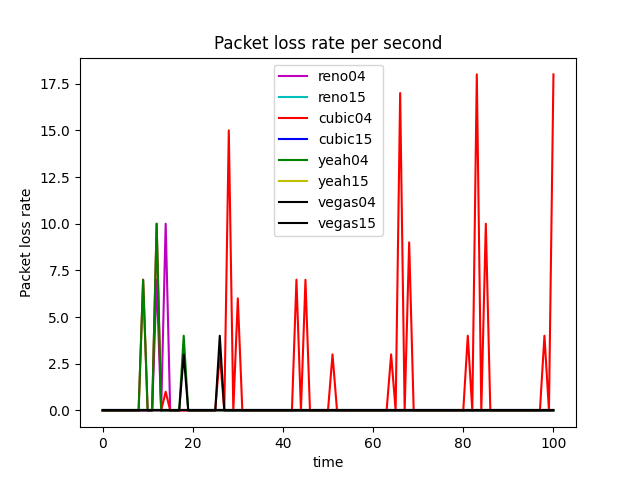
TCP Reno is an extension of TCP Tahoe, and their slow start and AIMD phase are the same. In TCP Reno, the cwnd is cyclically changed in a typical situation. The cwnd continues to increase until packet loss occurs. TCP Reno has two phases in increasing its cwnd: slow start phase and congestion avoidance phase . In othrt words, TCP Reno is composed of TCP Tahoe and fast recovery (see Figure 9).
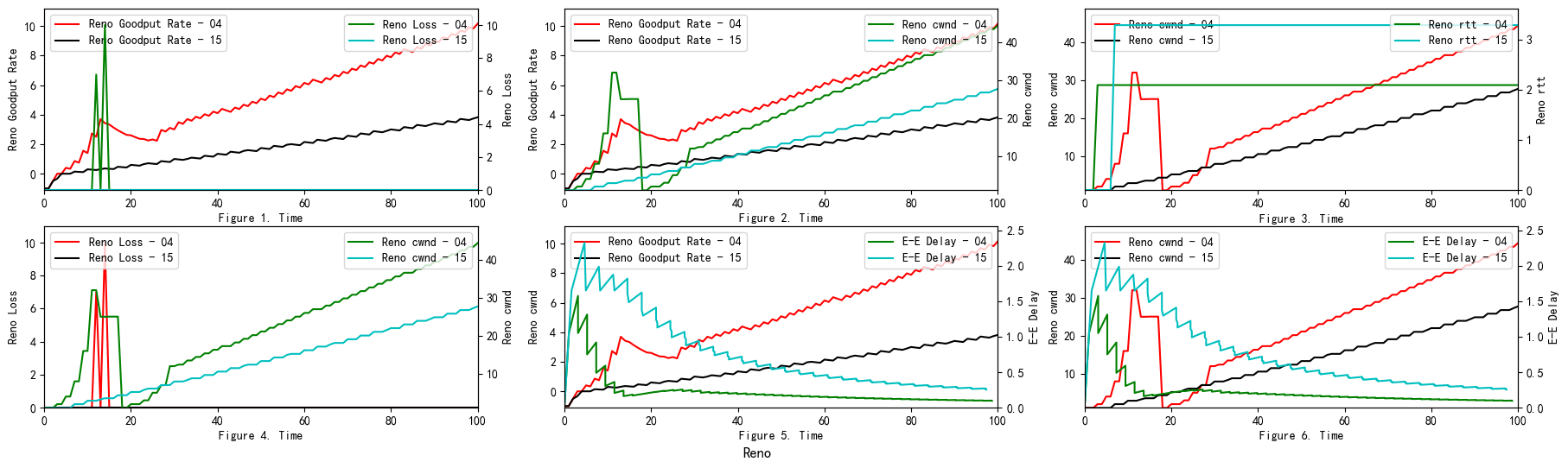
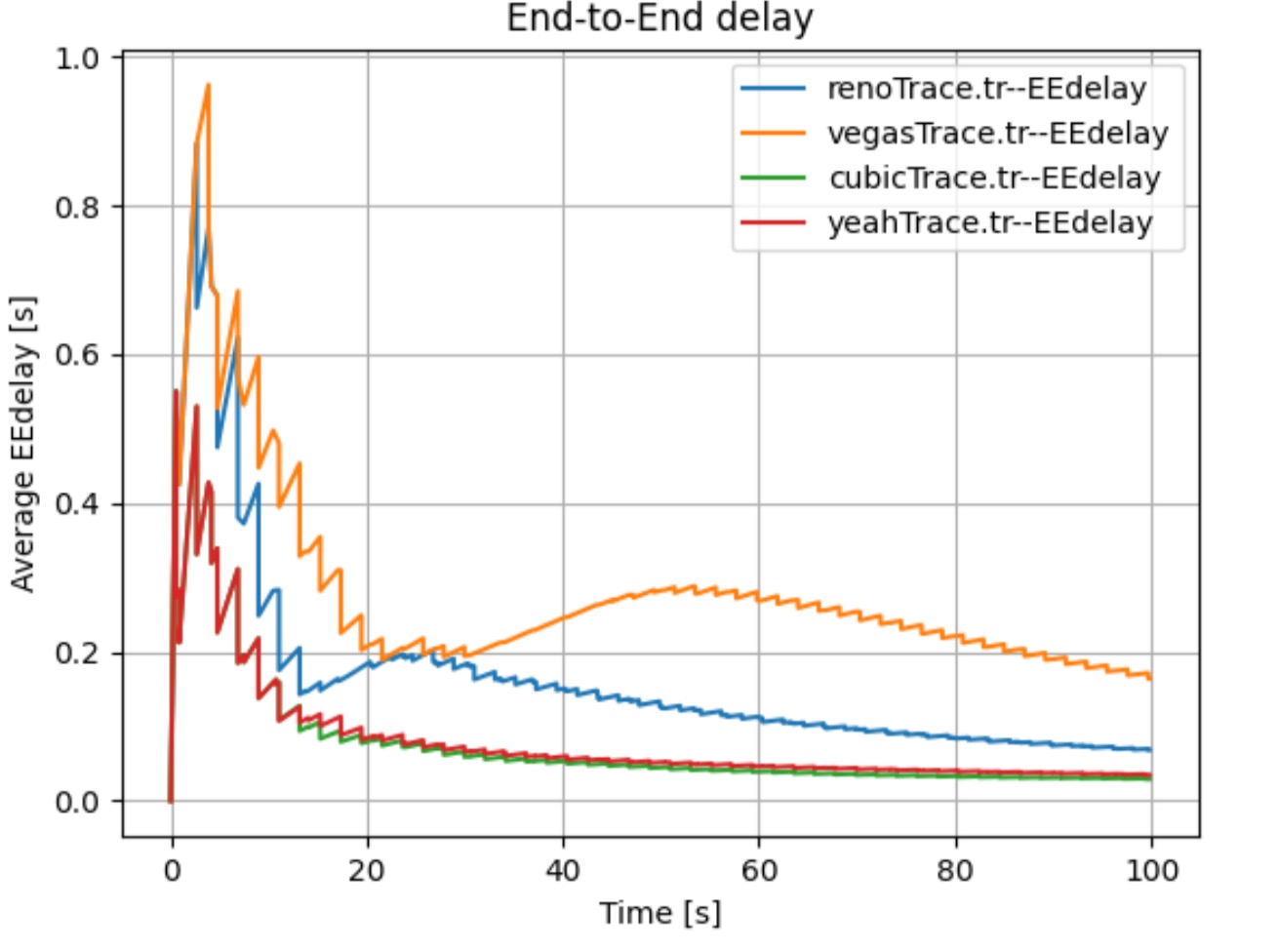
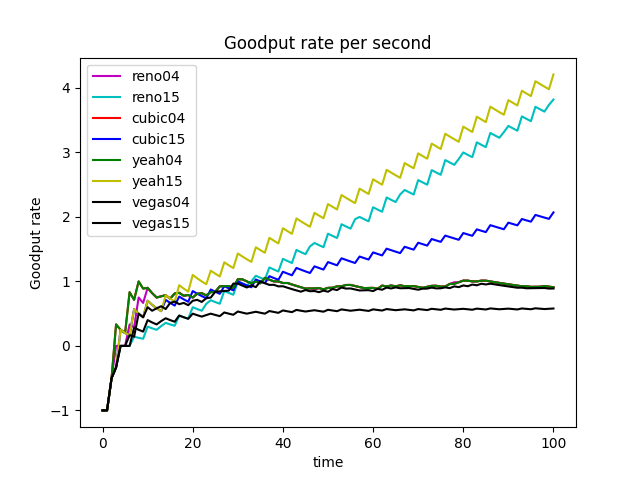
The GoodPut rate was unstable at the beginning due to the following reasons. Firstly, the beginning of the Reno algorithm is a slow start process, in which the cwnd increases exponentially, so the GoodPut rate also increases rapidly. Secondly, at around 15 seconds, the GoodPut is not stable enough because the cwnd increases too fast, and there is packet loss.
Moreover, the loss is not stable enough because, initially, the Reno algorithm needs to determine the value of cwnd based on the network conditions. Therefore, at 15 seconds, there is an excessive cwnd, which leads to packet loss.
The explanation also applies to other congestion control algorithms (Vegas, Cubic, Yeah).
TCP Vegas
TCP Reno models can determine the network’s congestion only when packet loss occurs in the system. In TCP Reno model, when packet loss occurs, the window size is decreased, and the system enters the congestion avoidance phase. While TCP Vegas senses the congestion in the network before any packet loss occurs, it instantly decreases the cwnd. Therefore, TCP Vegas handles the congestion without any packet loss occurring. $Extra~Data = (expectedOutput-actualOutput)baseRTT$ $\alpha \leq (expectedOutput-actualOutput)baseRTT \leq \beta$
-
If $Extra~Data > \beta$, Decrease Window Size, $cwnd=cwnd-1$
-
If $Extra~Data < \alpha$, Increase Window Size, $cwnd=cwnd+1$
-
If $\alpha \leq Extra~Data \leq \beta$, Maintaine Window Size, $cwnd=cwnd$
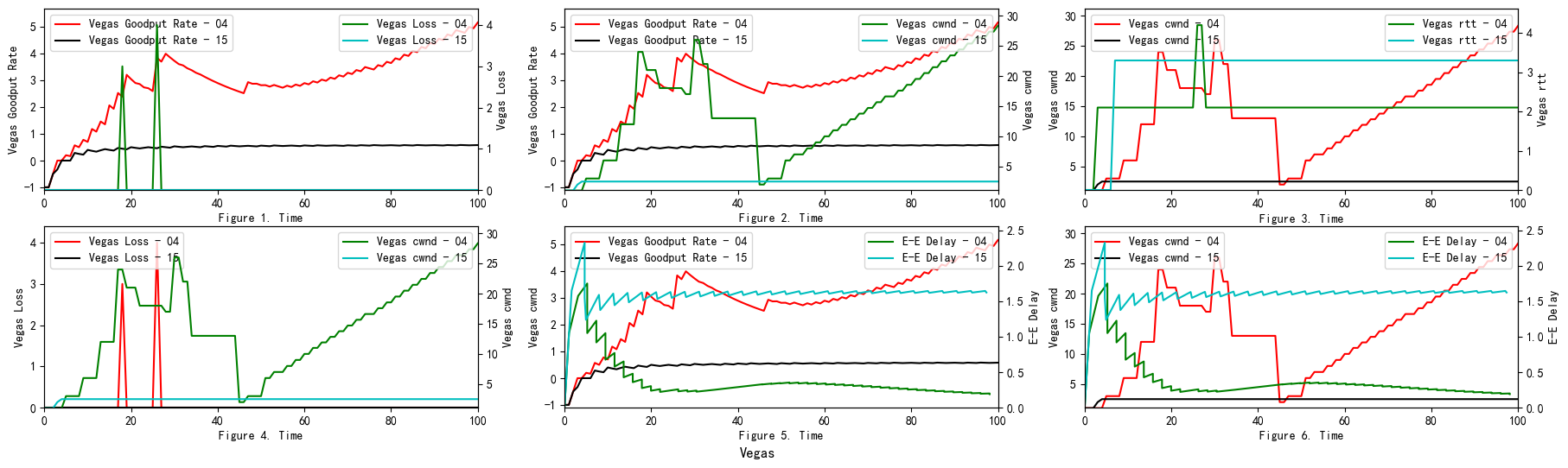
TCP Vegas attempts to utilize the network’s bandwidth without congestion in the network. The window size of TCP Vegas converges to the point that lies between $w + \alpha$ and $w + \beta$. TCP Vegas has congestion control ability and also gives stability to the network, but it can not fully use the bandwidth.
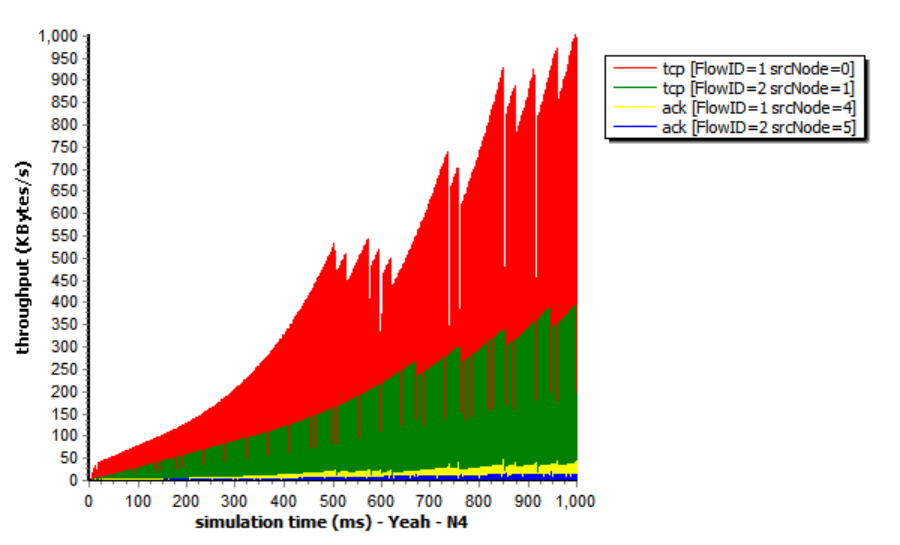
TCP YeAH
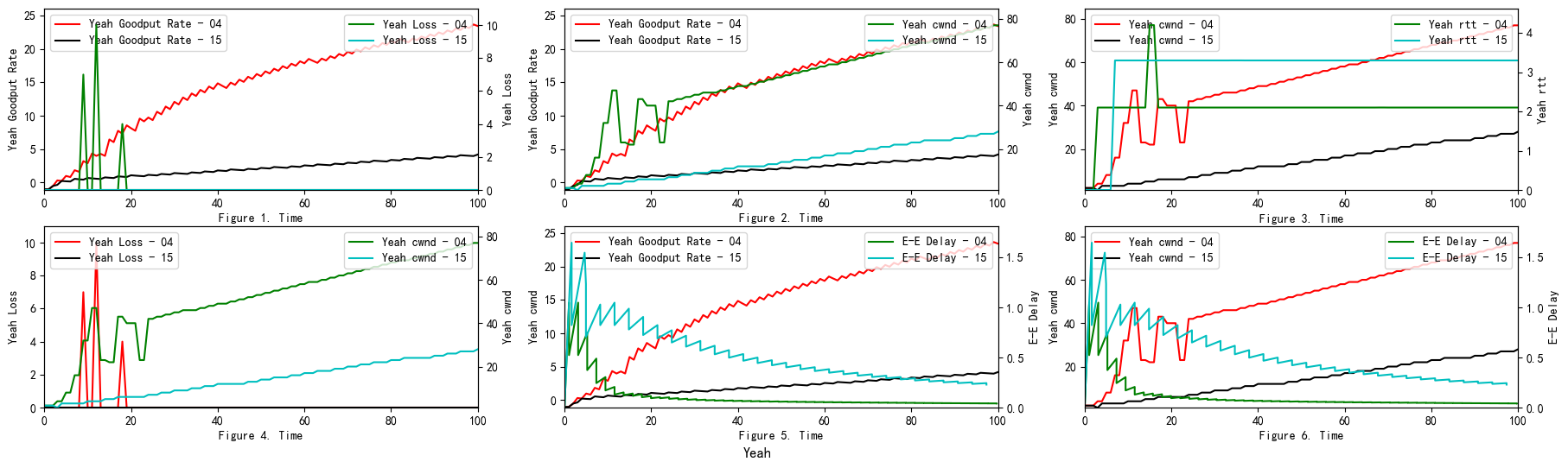
YeAH-TCP envisages two different operations: “Fast” and “Slow” modes, like Africa TCP. During the “Fast” mode, YeAH-TCP increments the cwnd according to an aggressive rule (STCP rule). In the “Slow” mode, it acts as Reno TCP.
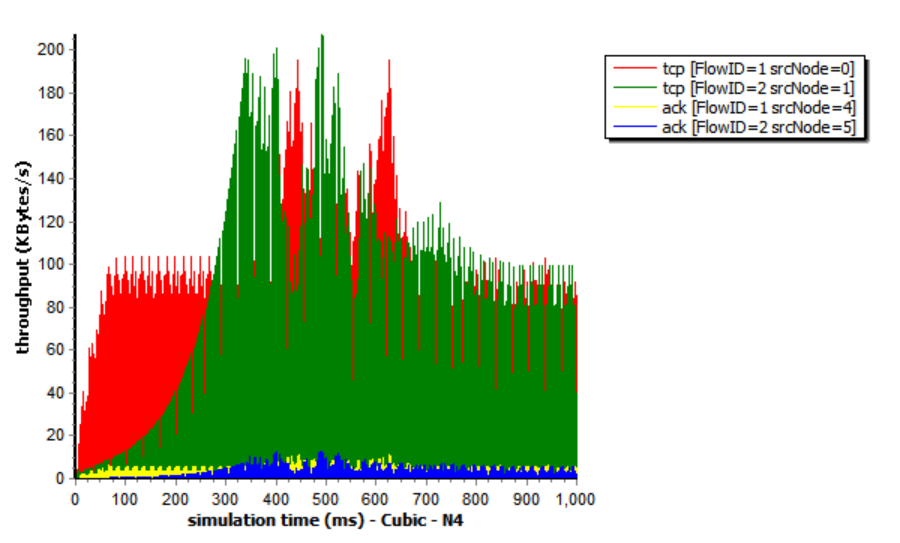
TCP Cubic
The window size in CUBIC is a cubic function of time since the most recent congestion event, with the inflection point set to the window size before the incident. The window growth function has two components because it is a cubic function. The window size quickly rises to the size prior to the most recent congestion incident in the first concave region. The convex expansion follows, where CUBIC initially searches for more bandwidth slowly and quickly. The network can stabilize because CUBIC spends a lot of time at a plateau between the concave and convex growth regions before it asks for more bandwidth.
What do you conclude after seeing these results? Which algorithm is better?
To decide which algorithm performs best, we analyze the trade-off of each algorithm at first.
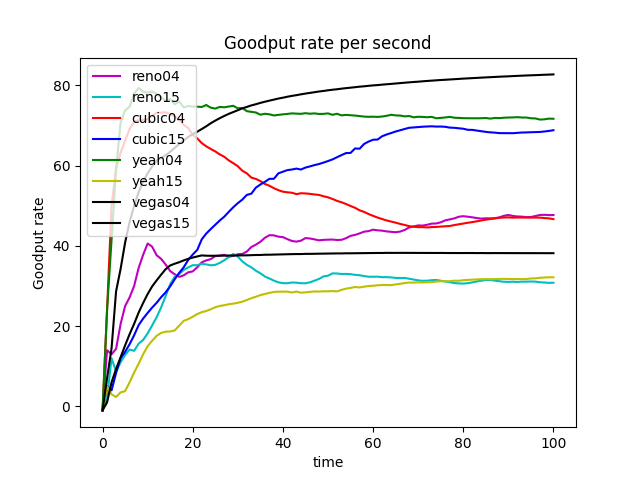
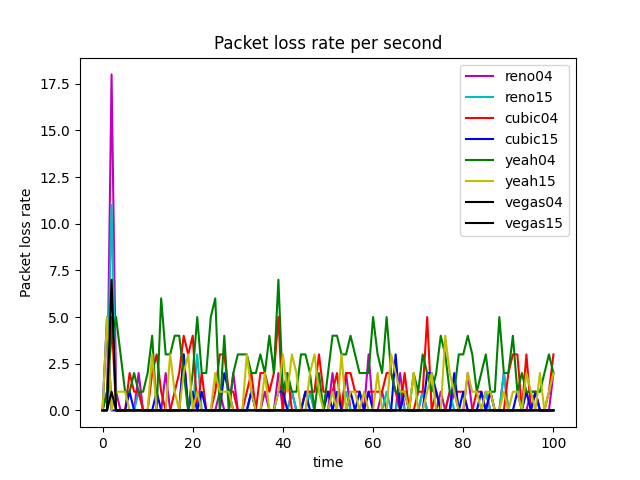
Reno algorithm is a conservative algorithm, which includes slow start, congestion avoidance, fast re-transmission, and fast recovery mechanisms. The cwnd of Reno algorithm decreases quickly and grows slowly, especially in the large-window environment. It takes a long time to recover the reduced cwnd caused by the loss of a datagram. In this way, the bandwidth utilization cannot be very high, and this disadvantage will become more and more obvious with the continuous improvement of the network link bandwidth. In terms of fairness, the Reno algorithm can fairly allocate resources so that one party does not occupy a large number of resources, resulting in insufficient resources for other nodes (see Figure 8).
The Vegas algorithm takes the increase of delay RTT as the signal of network congestion. The increase of RTT leads to decreased cwnd, and the decrease of RTT leads to an increased congestion window. Specifically, Vegas adjusts the size of the congestion window by comparing the actual throughput with the expected throughput. However, Vegas algorithm is inferior to Reno in fairness. For example, it can be seen in the Figure 10 that Vegas occupies much more bandwidth on link 04 than link 15. At the same time, the overall resource utilization of the algorithm is also relatively low.
The Yeah algorithm defines two patterns. Fast mode and Slow mode, which are more aggressive in Fast mode, behave the same way as Reno in Slow mode. It solves the problem that Reno algorithm can not use all the bandwidth and ensures fair and reasonable allocation of resources. At the same time, it also has a low packet loss rate (see Figure 11).
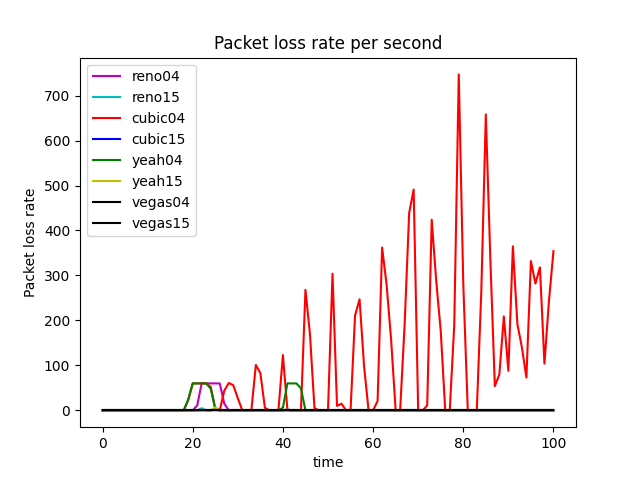
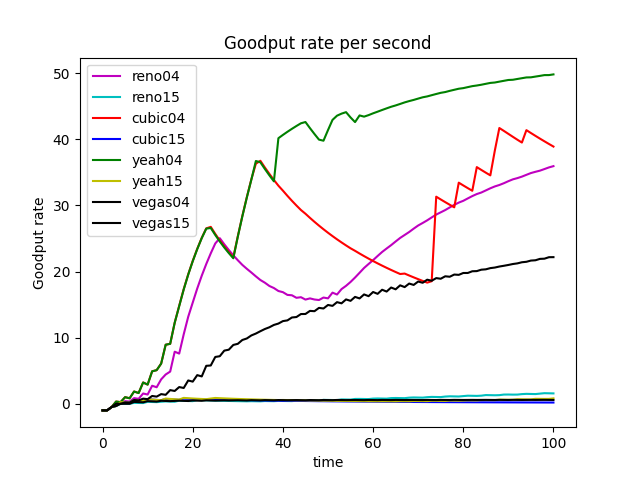
The advantage of the Cubic algorithm is that as long as there is no packet loss, it will not actively reduce its sending speed. It can maximize the remaining bandwidth of the network, improve the throughput, and play a better performance in the network with high bandwidth and low packet loss rate. However, while the Cubic algorithm has high bandwidth utilization, it still increases the cwnd, which indirectly increases the packet loss rate (see Figure 12), resulting in the aggravation of the network jitter.
Having discussed each algorithm’s features, we now analyze which one is better.
Each algorithm has its own advantages and disadvantages and applicable scenarios. In general, the Reno algorithm and Vegas are more conservative, which is also in line with its appearance in the early days of the Internet. Yeah algorithm solves part of the problems of the Reno algorithm, but in the case of high latency and high packet loss rate for a long time into Slow mode, and Reno algorithm is consistent. The cubic algorithm is more aggressive. The Cubic algorithm is more aggressive and has a higher packet loss rate, but it can guarantee high transmission speed in a poor network environment.
How reliable are these results, and how confident are you about the conclusion you have made based on these results?
To determine to which extent these results are reliable, we need to analyze the following aspects.
-
Reliable
- The simulation is performed in a real situation setting and therefore reflects the performance of the real situation under this specific condition.
-
Unreliable
-
The given simulation only lasts 100 seconds, which means the GoodPut rate may have not converged yet. Possible convergence will occur if time extends.
-
The parameters, such as bandwidth and latency, are not random enough to demonstrate the practical situation.
-
Since the simulation adapt TCP as the only protocol, the output may have a different result when utilizing HTTP, UDP or Telnet. Therefore, further experiments are required to verify the correctness.
-
The conditions for practical situations are more complex to set than in the simulation, so the results may not be reliable or indicative.
-
The setting of practical situations may change dynamically, so the results may not be reliable or indicative.
-
The parameters of current files only include Goodput rate and loss, which are insufficient.
-
How could you improve the confidence in your results?
To find an efficient way to improve the results based on the unreliable aspects written in Section 4.2, we conducted some experiments, including randomly established parameters and extending the testing duration.
-
To alleviate the random parameters or settings, we replace the Telnet protocol with the FTP protocol by changing the following code.
set mytelnet [new Application/Telnet] $mytelnet attach-agent $source1Then we compare the effectiveness of each algorithm (see Figure 23).
-
We avoid the problem that the experiment may not achieve the Extending the testing duration:
Goodput of Telnet 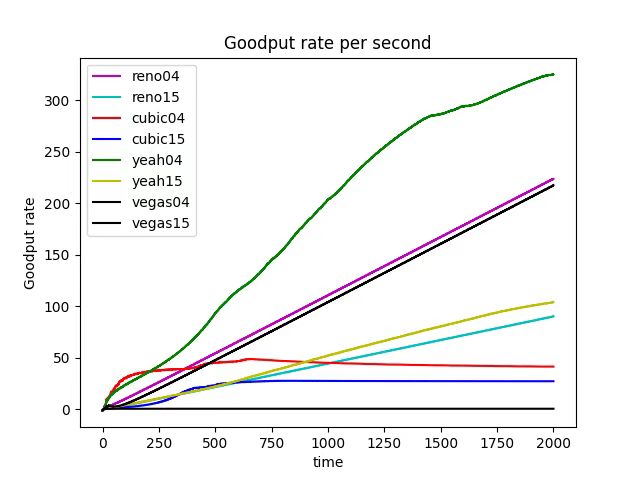
1000s - Goodput 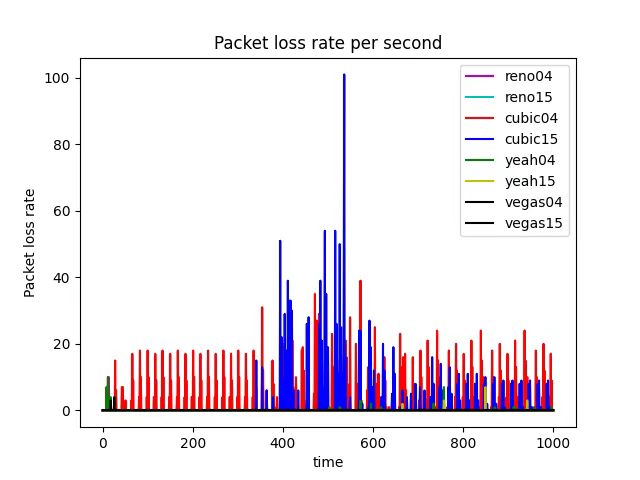
1000s - Loss 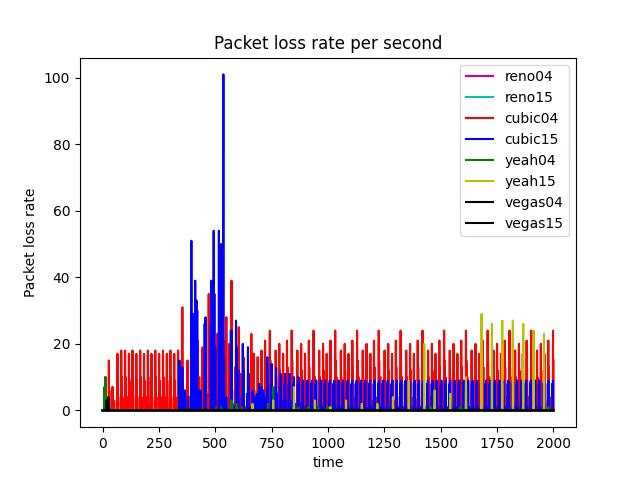
Extend to 2000s Impact of the bottleneck -
We solve the disadvantage of insufficient parameters by adding more parameters (see Figure 8, 10, 11, 12)
What is the equation used in “analyser.py” to calculate the GoodPut?
We calculate the number of ACK, which can be seen as the Goodput rate using Equation [goo], where $N$ represents the Number of ACK packets, $C$ represents Packet size, and $T$ represents the Measurement interval. $GoodPutRate = \frac{N \times C}{T} = \frac{d(N) \times C}{d(T)} = C \times \left(\frac{N}{T}\right)^{‘} \label{goo}$
Queuing Algorithms
Impact of the bottleneck link’s queuing algorithm - DropTail and RED
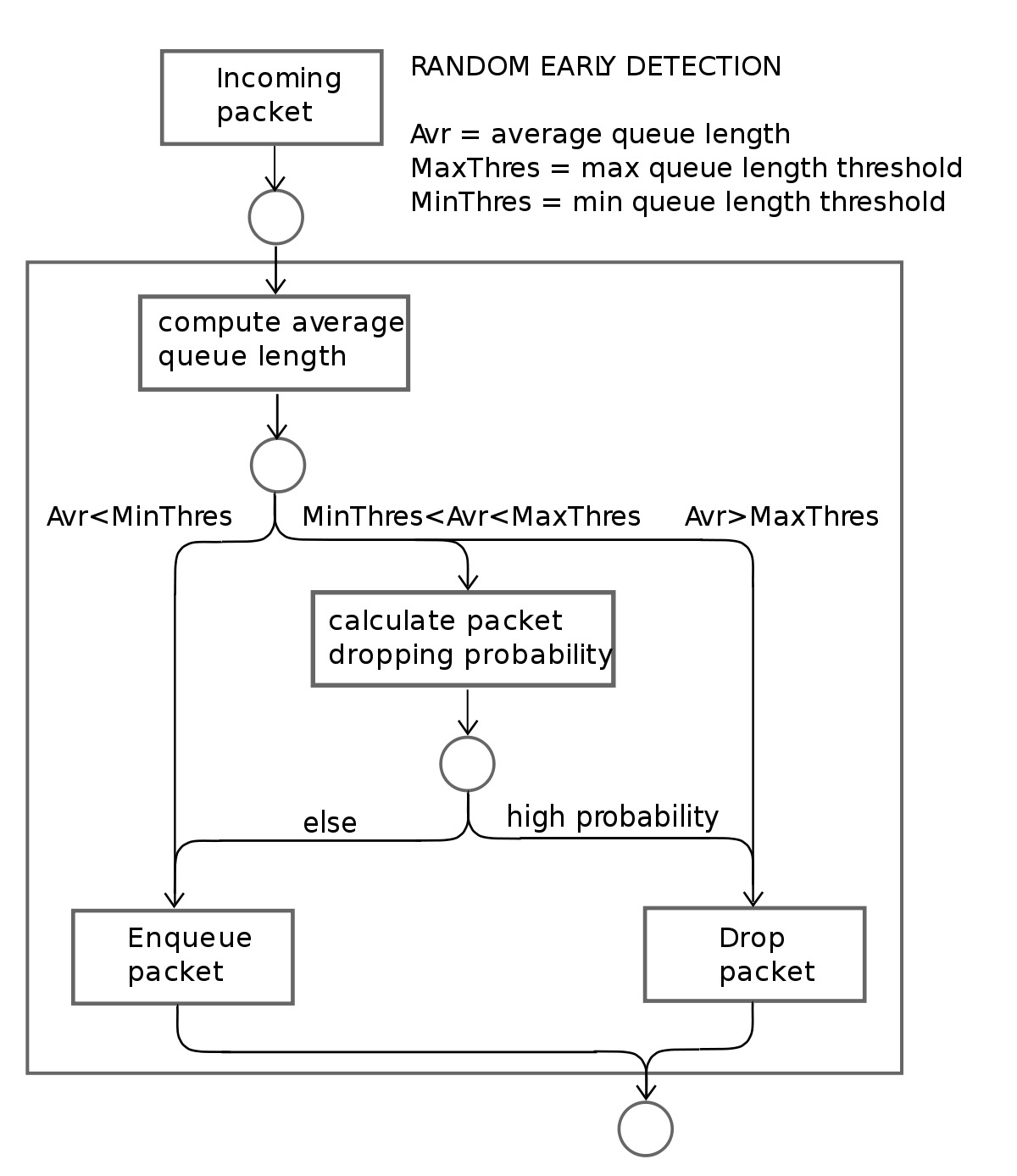
Random Early Detection (RED) loses packets in advance, while DropTail only loses packets when it reaches the maximum queue limit . Here are examples of how Cubic performs using different bottleneck link’s queuing algorithms (see Figure 21 and 22).
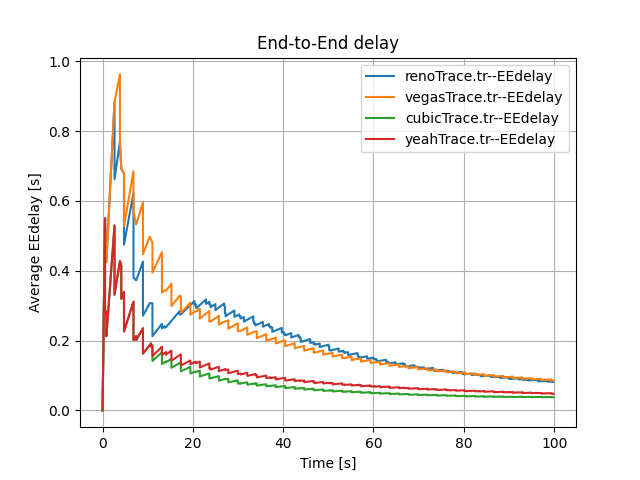
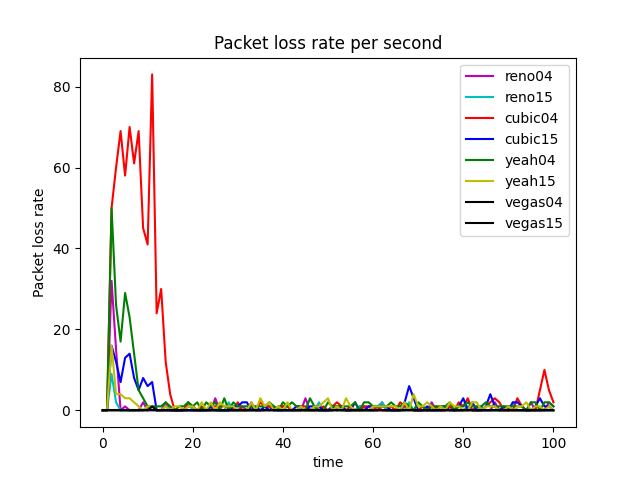
In the given experiments setting, when we compare Figure 17 (RED), Figure 1 (DropTail) and Figure 2 (DropTail), we can see that RED performs better than DropTail. This is because four different congestion control algorithms generally have lower end-to-end delays when using the RED bottleneck link’s queuing algorithm. Moreover, if we compare Figure 22 1 (RED) and Figure 21 1 (DropTail), we can see that DropTail performs better than RED in terms of Goodput rate.
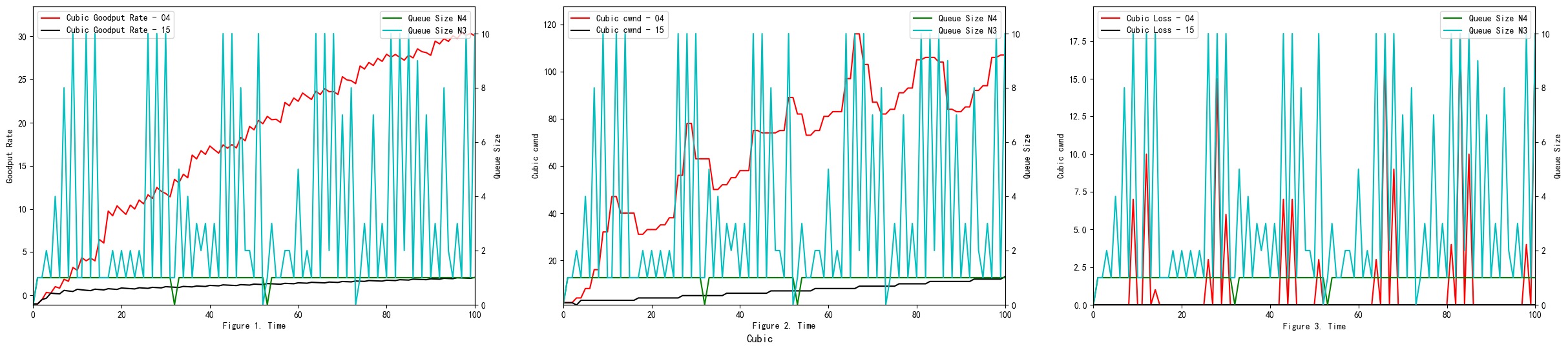
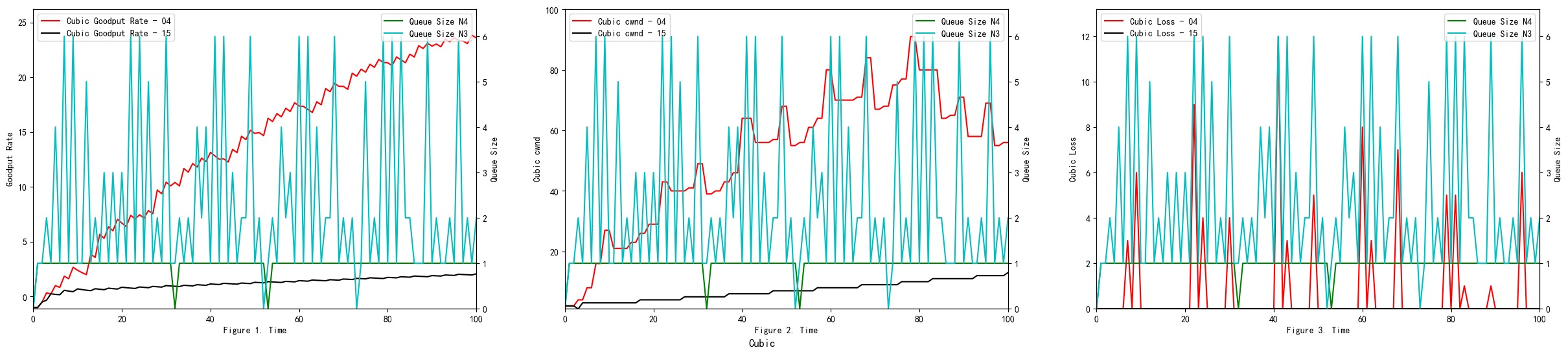
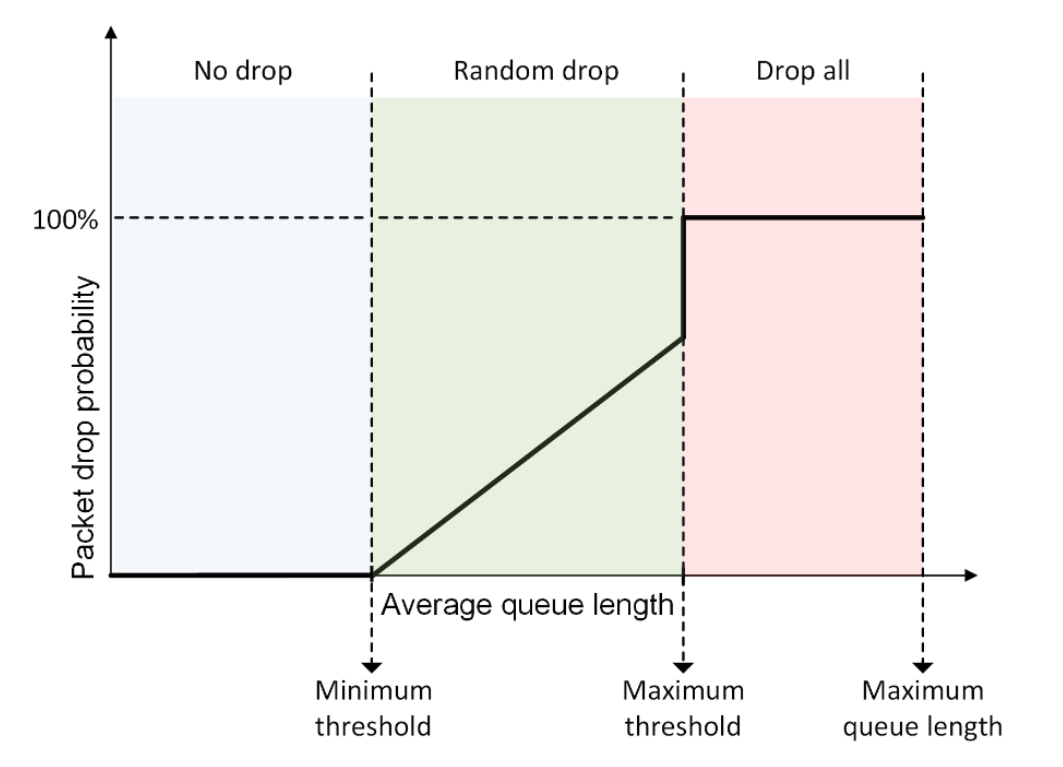
RED adds two new mechanisms to queue management. Firstly, instead of waiting for the queue to be full without dropping incoming packets, it uses a probabilistic determination mechanism to drop some packets in advance to prevent possible congestion. Secondly, it adjusts the packet drop probability by averaging the queues instead of instant queues. Therefore, it can absorb some transient bursts of traffic as much as possible. Moreover, the performance of the RED algorithm is sensitive to the design parameters and network conditions. These conditions can still lead to multiple TCP synchronization under specific network load conditions, resulting in throughput oscillations and increased delay jitter.
Repeat experiments with smaller and larger link capacity for the bottleneck link and discuss which algorithm worked better when congestion was worse
We noticed that in the given simulation scenario, the bandwidth as 1000Mb is not the bottleneck of this network (as shown in Figure 24), but the latency and queue size significantly affect the performance of the network.

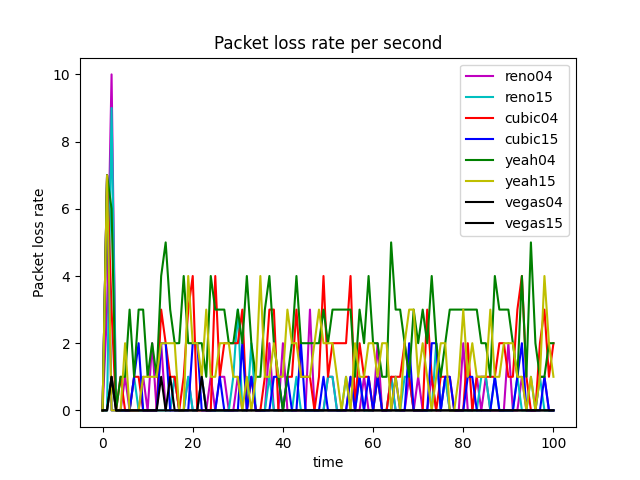
In this section, we change three different simulation scenarios and show that RED can perform much better in certain conditions.
Setting @ is shown in the following code block. As is shown in Figure 25 and Figure 27, RED performs better than DropTail because it has a lower average loss. Moreover, during the time interval 0-4s, all algorithms reach the highest packet loss. Similarly, RED also performs better than DropTail because it has a high average Goodput rate (see Figure 26 and 28). Specifically, RED is more stable than DropTail, as is illustrated in terms of both packet loss and Goodput rate (see Figure 29). For example, in Figure 28, Goodput rate, when applied to the DropTail algorithm, firstly increases and decreases when it reaches the peak at time 10s. In comparison, Goodput rate, when applied to the RED algorithm, remains a relatively stable high value. Therefore, in setting @, RED performs generally better than DropTail, which can be reflected by the less packet loss and higher Goodput rate of RED.
// It is not necessary to have a fast connection, but latency may significantly affect the network's performance.
// So we reduced the value of latency and speed; by doing this the transmission can reach the highest capacity of the bottleneck link.
$ns duplex-link $n1 $n3 4Mb 50ms DropTail
$ns duplex-link $n2 $n3 4Mb 80ms DropTail
$ns duplex-link $n3 $n4 1Mb 5ms DropTail // and RED
$ns duplex-link $n4 $n5 4Mb 50ms DropTail
$ns duplex-link $n4 $n6 4Mb 80ms DropTail
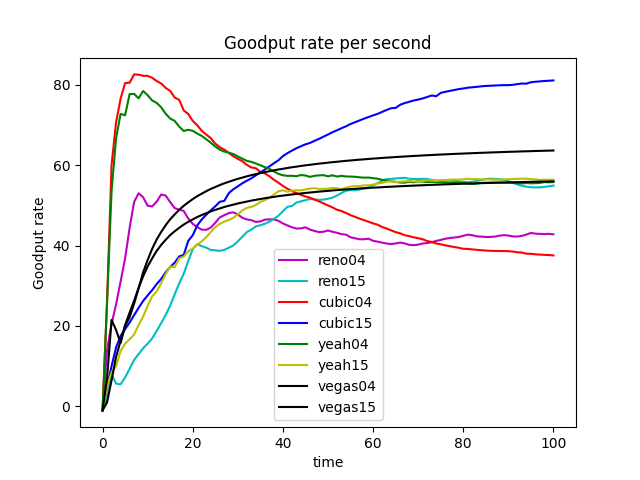
Setting @ is shown in the following code block. We also tried another setting and saw the result. As is shown in Figure 30 and 32, RED performs better than DropTail since it has a relatively lower average loss. Moreover, during the time interval 0-4s, all algorithms reach the highest packet loss. Similarly, RED also performs better than DropTail because it has a high average Goodput rate (see Figure 31 and 33). Specifically, RED is more stable than DropTail, as is illustrated in terms of both packet loss and Goodput rate (see Figure 34). For example, in Figure 33, Goodput rate, when applied to the DropTail algorithm, firstly increases and decreases when it reaches the peak at time 10s. In comparison, Goodput rate, when applied to the RED algorithm, remains a relatively stable high value. Therefore, in setting @, RED performs generally better than DropTail, which can be reflected by the less packet loss and higher Goodput rate of RED.
// RED algorithm considers the queue size. Thus, we set Queue limit to 100 and further reduced the speed of the bottleneck link.
$ns duplex-link $n1 $n3 4Mb 50ms DropTail
$ns duplex-link $n2 $n3 4Mb 80ms DropTail
$ns duplex-link $n3 $n4 0.5Mb 5ms DropTail // and RED
$ns duplex-link $n4 $n5 4Mb 50ms DropTail
$ns duplex-link $n4 $n6 4Mb 80ms DropTail
// Increase Queue Limit to 100
$ns queue-limit $n3 $n4 100
$ns queue-limit $n4 $n3 100
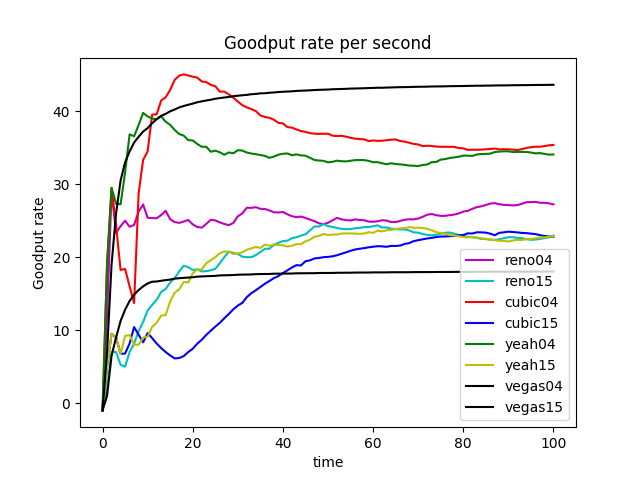
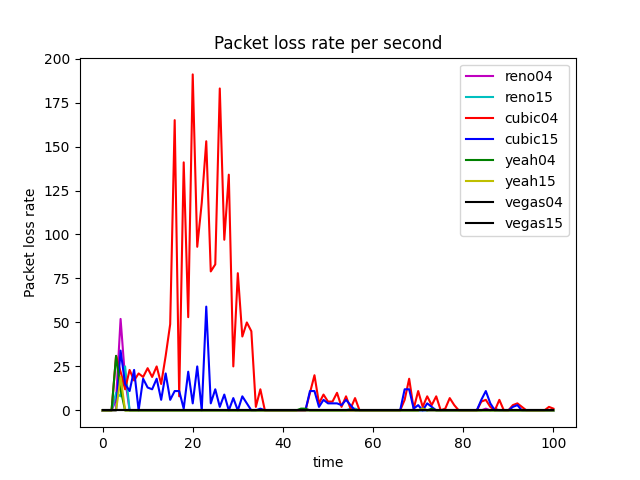
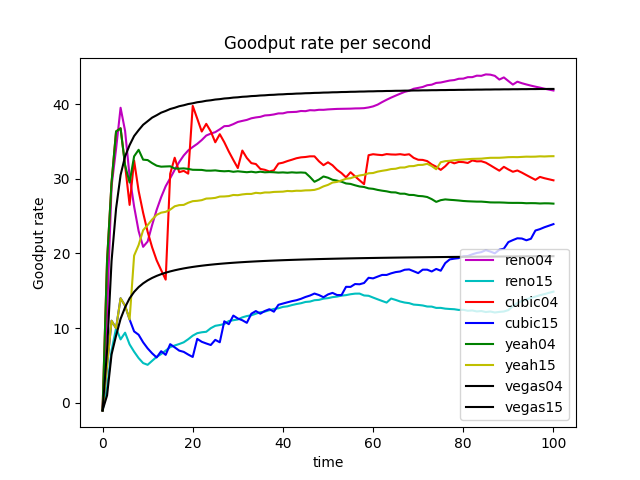
Setting @ is shown in the following code block. We also try another setting and see the result. As is shown in Figure 35 and 37, RED performs better than DropTail since it has a remarkably lower loss. Similarly, RED also performs better than DropTail because it has a high Goodput rate (see Figure 36 and 38). Specifically, RED is more stable than DropTail, as is illustrated in terms of both packet loss and Goodput rate (see Figure 39). For example, in Figure 38, Goodput rate, when applied to the DropTail algorithm, firstly increases and decreases and then shows an increasing trend again. In comparison, Goodput rate, when applied to the RED algorithm, remains a relatively stable ascending trend. Therefore, in setting @, RED performs generally better than DropTail, which can be reflected by the less packet loss and higher Goodput rate of RED.
// Here, we simulated a really poor network connection where the latency and connection speed were high.
$ns duplex-link $n1 $n3 4Mb 500ms DropTail
$ns duplex-link $n2 $n3 4Mb 800ms DropTail
$ns duplex-link $n3 $n4 0.5Mb 50ms DropTail // and RED
$ns duplex-link $n4 $n5 4Mb 500ms DropTail
$ns duplex-link $n4 $n6 4Mb 800ms DropTail
// Increase Queue Limit to 200
$ns queue-limit $n3 $n4 200
$ns queue-limit $n4 $n3 200